Binary Heap
자료구조의 일종으로 Tree 의 형식을 하고 있으며, Tree 중에서도 배열에 기반한 Complete Binary Tree이다. 배열에 트리의 값들을 넣어줄 때, 0 번째는 건너뛰고 1 번 index 부터 루트노드가 시작된다. 이는 노드의 고유번호 값과 배열의 index 를 일치시켜 혼동을 줄이기 위함이다. 힙(Heap)에는 최대힙(max heap), 최소힙(min heap) 두 종류가 있다.
Max Heap이란, 각 노드의 값이 해당 children 의 값보다 크거나 같은 complete binary tree를 말한다. ( Min Heap 은 그 반대이다.)
Max Heap에서는 Root node 에 있는 값이 제일 크므로, 최대값을 찾는데 소요되는 연산의 time complexity 이 O(1)이다. 그리고 complete binary tree이기 때문에 배열을 사용하여 효율적으로 관리할 수 있다. (즉, random access 가 가능하다. Min heap 에서는 최소값을 찾는데 소요되는 연산의 time complexity 가 O(1)이다.) 하지만 heap 의 구조를 계속 유지하기 위해서는 제거된 루트 노드를 대체할 다른 노드가 필요하다. 여기서 heap 은 맨 마지막 노드를 루트 노드로 대체시킨 후, 다시 heapify 과정을 거쳐 heap 구조를 유지한다. 이런 경우에는 결국 O(log n)의 시간복잡도로 최대값 또는 최소값에 접근할 수 있게 된다.
Personal Recommendation
- Heapify 구현하기
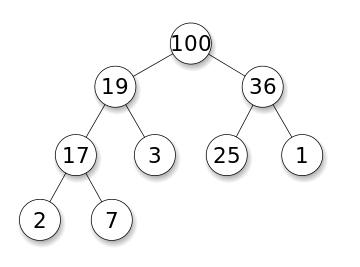

참고 : en.wikipedia.org/wiki/Binary_heap
출처 : github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/DataStructure#stack-and-queue